Speeding Up Median String Finding Algorithm

Table of Contents

Understanding Motifs and K-mers
Initial Implementation in Python
Optimized Implementation in Go
Parallelization
Conclusion

Understanding Motifs and K-mers

In bioinformatics, a motif is a short, recurring pattern in DNA, RNA, or protein sequences that is biologically significant. Motifs are often associated with specific biological functions and can indicate regulatory elements, binding sites for proteins, or conserved regions within a sequence.

A k-mer is a substring of length k from a longer DNA, RNA, or protein sequence. For example, in the DNA sequence "AGCTG", the 3-mers (substrings of length 3) are "AGC", "GCT", and "CTG". K-mers are used in many bioinformatics analyses, including sequence alignment, and motif discovery. By analyzing the frequency and distribution of k-mers within a sequence or across multiple sequences, researchers can identify conserved regions, detect sequence variations, and understand evolutionary relationships.

Initial Implementation in Python

The task of finding the median string can be computationally intensive, particularly when implemented using a brute force (trying all k-mers one by one) approach in Python or input size is very large. Here is the initial slightly improved implementation of the algorithm:

from itertools import product
from typing import List


def hamming_distance(s1: str, s2: str) -> int:
    distance = 0
    n = len(s1)

    for i in range(n):
        if s1[i] != s2[i]:
            distance += 1

    return distance

def min_hamming_distance(kmer: str, dna_string: str) -> int:
    min_distance = len(kmer)
    
    for i in range(len(dna_string) - len(kmer) + 1):
        distance = hamming_distance(kmer, dna_string[i:i + len(kmer)])
        if distance < min_distance:
            min_distance = distance
    
    return min_distance

def extract_kmers(k: int, dna_strings: List[str]) -> List[str]:
    kmers = []
    
    for dna_string in dna_strings:
        for i in range(len(dna_string) - k + 1):
            kmers.append(dna_string[i:i+k])
    
    return kmers

def find_median_string(k: int, dna_strings: List[str]) -> str | None:
    # Extract all possible kmers at length k
    kmers = extract_kmers(k, dna_strings)
    min_sum = len(dna_strings) * len(kmers)
    result = None

    for kmer in kmers:
        sum_distance = 0

        for j in range(len(dna_strings)):
            sum_distance += min_hamming_distance(kmer, dna_strings[j])

        # If the current kmer gives has a lower sum of distance choose it
        if sum_distance < min_sum:
            min_sum = sum_distance
            result = kmer

    return result

This slightly improved version runs with the k-mers extracted from DNA strings rather than generating all possible combinations.

I benchmarked the code with 10 DNA sequences (each with 500 nucleotides), resulting in a total data size of 5000 characters. Each benchmark was run 10 times, and the average time was recorded.

k-mer length	Average Time Spent (ms)
7	11187
8	11893
9	12692

Optimized Implementation in Go

Choice of Go

Python is popular in the bioinformatics field, but I believed that I could make this algorithm much faster by using a compiled language. Due to my familiarity with Go and its power to allow developing concurrent or parallel programs, I chose Go for the optimized implementation.

Initial Go Implementation

Here is the initial Go implementation of the same algorithm:

package medianstring

import (
	"runtime"
	"sync"
)

func hammingDistance(s1, s2 string) int {
	distance := 0

	for i := range s1 {
		if s1[i] != s2[i] {
			distance++
		}
	}

	return distance
}

func minHammingDistance(kmer, dnaString string) int {
	minDistance := len(kmer)

	for i := 0; i < len(dnaString)-len(kmer)+1; i++ {
		distance := hammingDistance(kmer, dnaString[i:i+len(kmer)])
		if distance < minDistance {
			minDistance = distance
		}
	}

	return minDistance
}

func extractKmers(k int, dnaStrings []string) []string {
	cap := len(dnaStrings) * (len(dnaStrings[0]) - k + 1)
	kmers := make([]string, 0, cap)

	for _, dnaString := range dnaStrings {
		for i := 0; i < len(dnaString)-k+1; i++ {
			kmers = append(kmers, dnaString[i:i+k])
		}
	}

	return kmers
}

func Find(k int, dnaStrings []string) string {
	kmers := extractKmers(k, dnaStrings)
	minSum := len(kmers) * len(dnaStrings)
	result := ""

	for _, kmer := range kmers {
		sum := 0

		for _, dnaString := range dnaStrings {
			sum += minHammingDistance(kmer, dnaString)
			if sum >= minSum {
				break
			}
		}

		if sum < minSum {
			minSum = sum
			result = kmer
		}
	}

	return result
}

The Go implementation showed a significant improvement in performance.

k-mer length	Average Time Spent (ms)
7	85
8	115
9	136
In average the Go version run ~10 times faster than the Python version and I have not made any improvement in the algorithm yet.

Parallelization

Parallel Implementation in Go

To further optimize the algorithm, I took advantage of parallel processing. This allows the minimum hamming distance for each k-mer to be computed in separate goroutines. The results are then sent to a channel in a custom struct.

func FindParallel(k int, dnaStrings []string) string {
	kmers := extractKmers(k, dnaStrings)
	minSum := len(kmers) * len(dnaStrings)
	result := ""

	type kmerAndSum struct {
		sum  int
		kmer string
	}

	ch := make(chan *kmerAndSum)
	var wg sync.WaitGroup

	for _, kmer := range kmers {
		wg.Add(1)

		go func(kmer string) {
			defer wg.Done()

			sum := 0
			for _, dnaString := range dnaStrings {
				sum += minHammingDistance(kmer, dnaString)
			}

			ch <- &kmerAndSum{
				sum:  sum,
				kmer: kmer,
			}
		}(kmer)
	}

	go func() {
		wg.Wait()
		close(ch)
	}()

	for kmerAndSum := range ch {
		if kmerAndSum.sum >= minSum {
			continue
		}
		minSum = kmerAndSum.sum
		result = kmerAndSum.kmer
	}

	return result
}

Parallelizing the computation further reduced the execution time.

k-mer length	Average Time Spent (ms)	Change (%)
7	43	-49.41
8	46	-60.00
9	49	-63.97
So, parallezing works. Why not use it in the other places? We can extract k-mers from DNA's simulteneously.

func extractKmersParallel(k int, dnaStrings []string) <-chan string {
	ch := make(chan string)
	var wg sync.WaitGroup

	for _, dnaString := range dnaStrings {
		wg.Add(1)

		go func(dnaString string) {
			defer wg.Done()

			for i := 0; i <= len(dnaString)-k; i++ {
				ch <- dnaString[i : i+k]
			}
		}(dnaString)
	}

	go func() {
		wg.Wait()
		close(ch)
	}()

	return ch
}

The results a bit unexpected to me. It did not make a significant change on the runtime performance.

k-mer length	Average Time Spent (ms)
7	44
8	47
9	51
I thought that it might be related to the `wg.Wait` inside the `extractKmersParallel`. Because it prevents `FindParallel` from processing k-mers simulteneuosly. I have changed the implementation and now it returns the k-mers channel immediately, without waiting until all DNAs are processed.

func extractKmersParallel2(k int, dnaStrings []string) <-chan string {
	ch := make(chan string)

	go func() {
		defer close(ch)

		for _, dnaString := range dnaStrings {
			for i := 0; i <= len(dnaString)-k; i++ {
				ch <- dnaString[i : i+k]
			}
		}
	}()

	return ch
}

It did not improved the performance even though it made it worse.

k-mer length	Average Time Spent (ms)	Change (%)
7	52	+18.19
8	54	+14.89
9	56	+9.80
As it does not have a positive effect on the performance I switched back to the previous version.

Additional Optimizations

Early Exit Conditions

Let's put aside playing with goroutines and look at how can we improve the main algorithm. We try to find the k-mer with the minimum hamming distance sum. So, if the current some goes over the current minimum we do not need to keep going the comparison. To early exit I have passed the current minimum inside the goroutine and if the calculated sum goes over it, it returns without continuing to the calculation.

go func(kmer string, minSum int) {
	defer wg.Done()

	sum := 0
	for _, dnaString := range dnaStrings {
		sum += minHammingDistance(kmer, dnaString)
		if sum >= minSum {
			break
		}
	}

	if sum >= minSum {
		return
	}

	ch <- &kmerAndSum{
		sum:  sum,
		kmer: kmer,
	}
}(kmer, minSum)

This time I compare the results with the first parallel version of extractKmers.

k-mer length	Average Time Spent (ms)	Change (%)
7	44	0.00
8	48	+2.13
9	51	0.00

To find more rooms for improvement I run the program with CPU profiling.

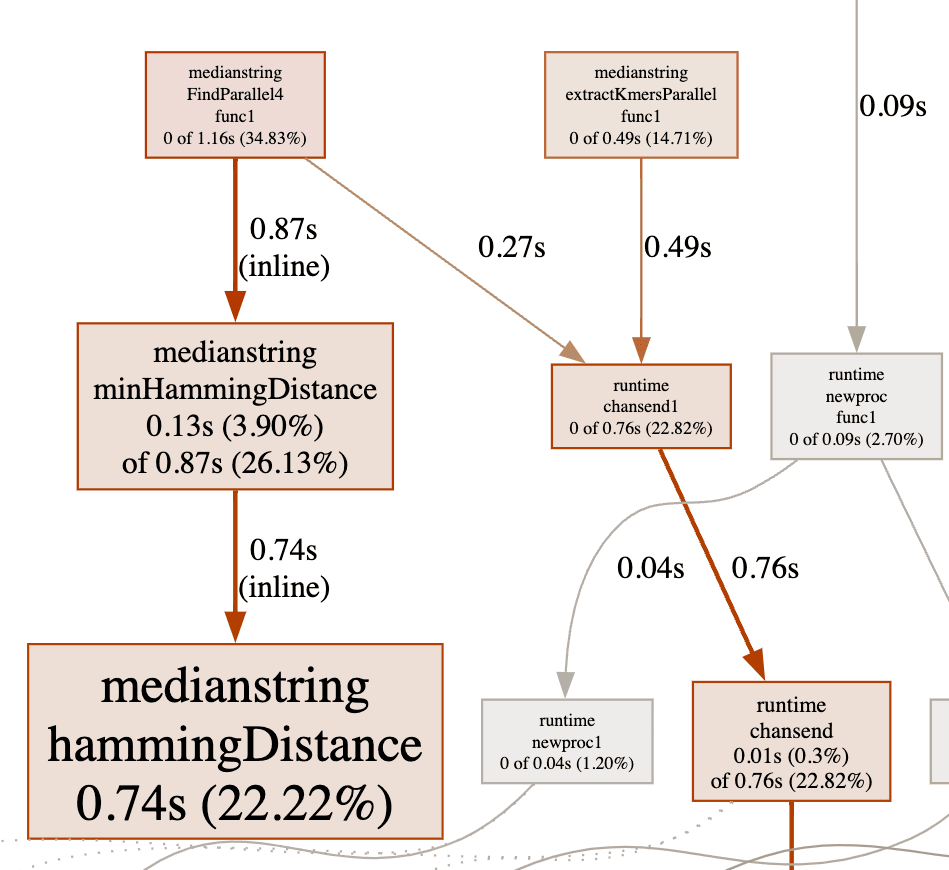
According to the profiling result hammingDistance function takes significant amount of time. I have inlined the hammindDistance algorithm and added some early exit conditions -if the current distance exceed the current minimum it stops iterating-.

func minHammingDistance2(kmer, dnaString string) int {
	kmerLen := len(kmer)
	dnaLen := len(dnaString)

	minDistance := kmerLen

	for i := 0; i <= dnaLen-kmerLen; i++ {
		distance := 0
		for j := 0; j < kmerLen; j++ {
			if kmer[j] != dnaString[i+j] {
				distance++
				if distance >= minDistance {
					break
				}
			}
		}

		if distance < minDistance {
			minDistance = distance
			if minDistance == 0 {
				break
			}
		}
	}

	return minDistance
}

And the new profiling graph looks like this.

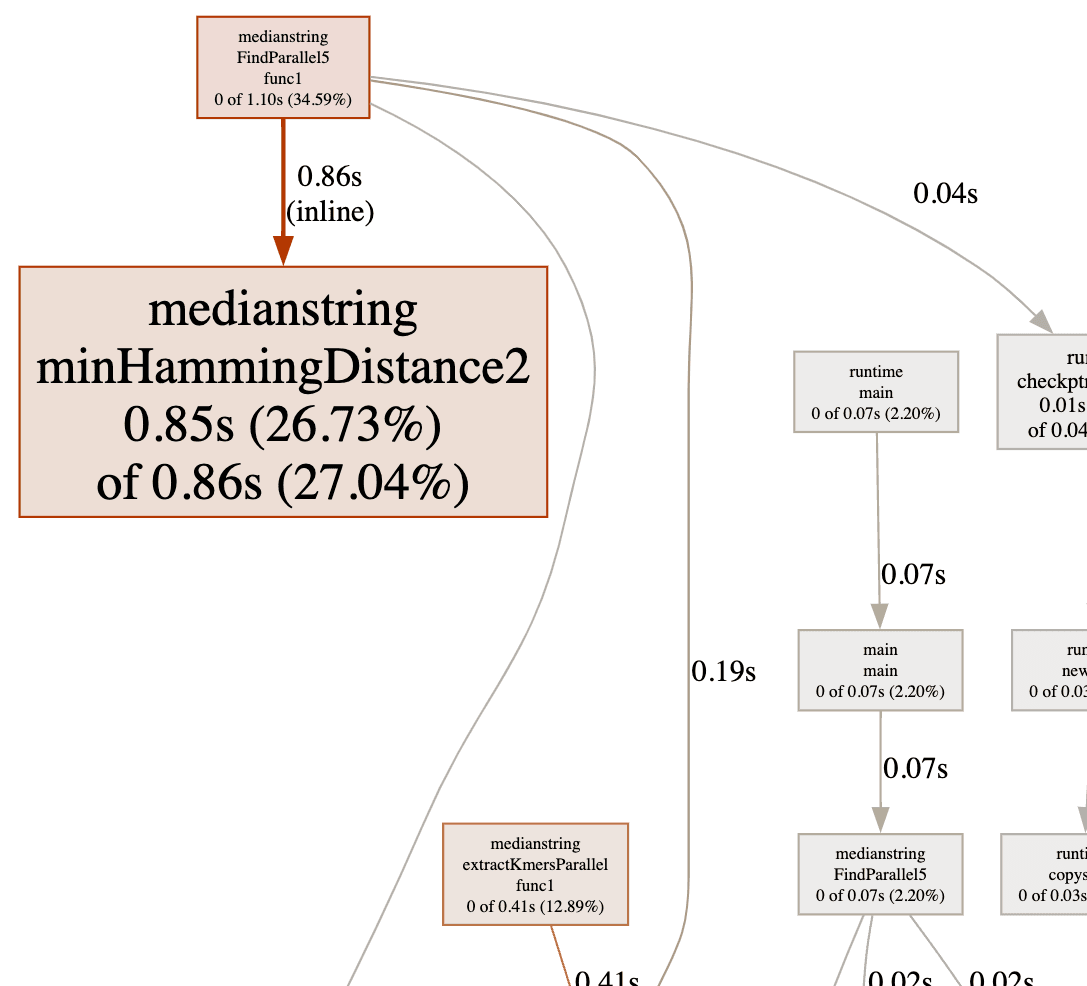
improved median string finding cpu profiling

k-mer length	Average Time Spent (ms)	Change (%)
7	41	-6.82
8	45	-4.26
9	52	+1.96

Binary Encoding DNA Strings

It is the slowest part of the code. And as we all know computers are better at arithmetic operations rather than string operations. This made me want to try with binary encoded DNAs. Then I could compute the hamming distance by just only bitwise operations.

func encodeDNA(dna string) uint64 {
	var result uint64
	for _, nucleotide := range dna {
		result <<= 2
		switch nucleotide {
		case 'A':
			// 00
		case 'C':
			result |= 1 // 01
		case 'G':
			result |= 2 // 10
		case 'T':
			result |= 3 // 11
		}
	}
	return result
}

func minHammingDistanceBitwise(kmer, dnaString string) int {
	kmerLen := len(kmer)
	dnaLen := len(dnaString)

	minDistance := kmerLen
	encodedKmer := encodeDNA(kmer)

	for i := 0; i <= dnaLen-kmerLen; i++ {
		encodedDnaSegment := encodeDNA(dnaString[i : i+kmerLen])
		distance := bits.OnesCount64(encodedKmer ^ encodedDnaSegment)

		if distance < minDistance {
			minDistance = distance
			if minDistance == 0 {
				break
			}
		}
	}

	return minDistance
}

median string finding with binary encoded dna cpu profiling

k-mer length	Average Time Spent (ms)	Change (%)
7	17	-58.54
8	19	-57.78
9	26	-50.00

Conclusion

By implementing the median string finding algorithm in Go and utilizing parallel processing and binary encoding techniques, we achieved significant performance improvements. Future work could explore further optimizations and the application of these techniques to other computational problems in bioinformatics.